Area under a curve

Area under a curve

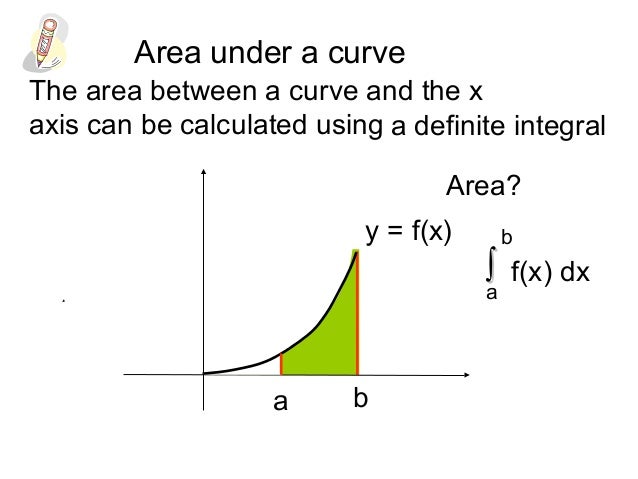
The Area Under a Curve. The area under a curve between two points can be found by doing a definite integral between the two points. To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b. Areas under the x-axis will come out negative and areas above the x-axis will be positive The area under a curve between two points is found out by doing a definite integral between the two points. To find the area under the curve y = f(x) between x = a & x = b, integrate y = f(x) between the limits of a and b. This area can be calculated using integration with given limits. Formula to Calculate the Area Under a Curve Mar 06,  · We can show in general, the exact area under a curve y = f(x) from. x = a. \displaystyle {x}= {a} x = a to. x = b. \displaystyle {x}= {b} x = b is given by the definite integral: A r e a = ∫ a b f (x) d x. \displaystyle\text {Area}= {\int_ { {a}}^ { {b}}} f { {\left ({x}\right)}} {\left. {d} {x}\right.} Area = ∫ ab

Calculus - Area under a Curve (video lessons, examples, solutions)

So far when integrating, there has always been a constant term left. For this reason, such integrals are known as indefinite integrals. With definite integrals, we integrate a function between 2 points, and so we can find the precise value of the integral and there is no need area under a curve any unknown constant terms [the constant cancels out].

The area under a curve between two points can be found by doing a definite integral between the two points. Areas under the x-axis will come out negative and areas above the x-axis will be positive. This means that you have to be careful when finding an area which is partly above and partly below the x-axis.

You may also be asked to find the area between the curve and the y-axis. To do this, integrate with respect to y. Copyright © - Revision World Networks Ltd.

Skip to main content. Search form. Sign up Log in, area under a curve. GCSE MATHS A-LEVEL MATHS GCSE to A-Level Pure Maths Statistics Mechanics A-Level Maths Past Papers Other A-Level Subjects My Timetable Revision Science Revision World Revision Videos Student Jungle. Home A-LEVEL MATHS Pure Maths Calculus Area Under a Curve.

Area Under a Curve Calculating the area under a curve. Definite Integrals So far when integrating, area under a curve, there has always been a constant term left. The Area Under a Curve The area under a curve between two points can be found by doing a definite integral area under a curve the two points.

Home About Us Advertise with us Cookies Policy Privacy Policy.

Areas by Integration (1 of 6: Basic area under curve)

, time: 11:48

Area Under A Curve

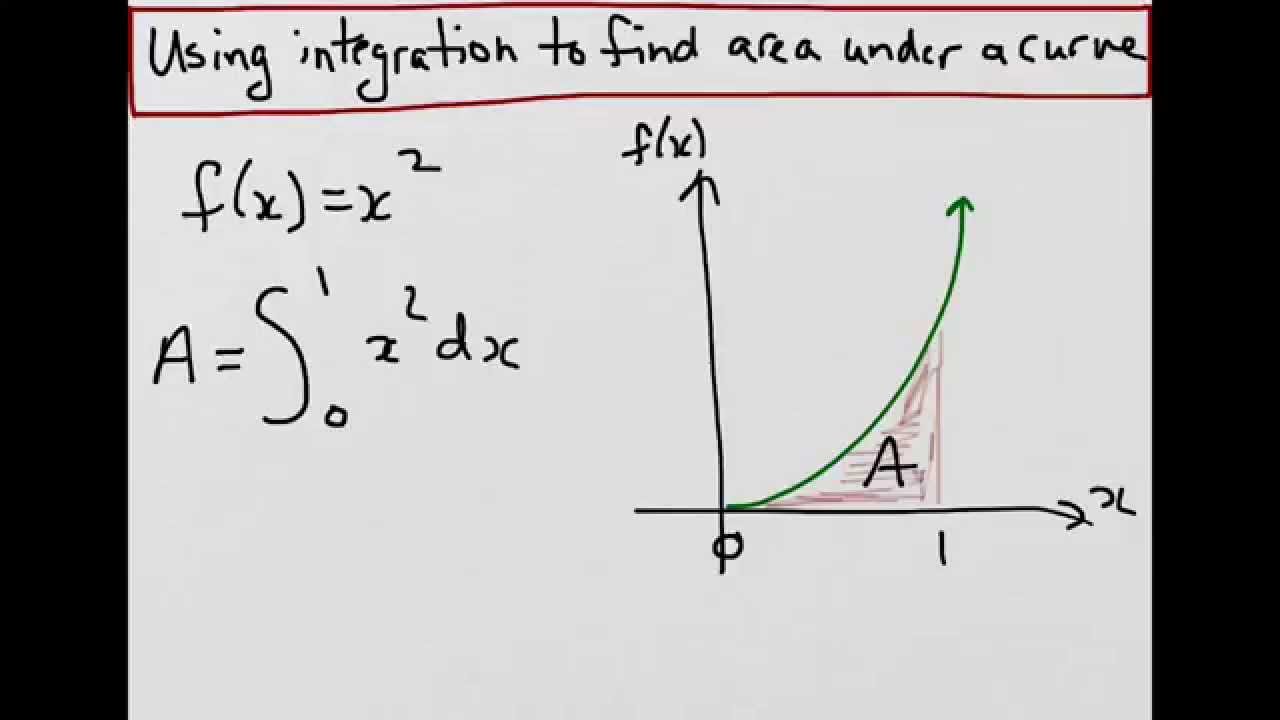
Total Area under the curve. 4. Slivers under the curve are green (click the circle below). 6. Partial Area under the curve 7. The a-slider is the width of each sliver. The b-slider is the gap between slivers. a = 0. 5. powered by. powered by "x" $$ x "y" $$ y "a" squared Formula For Area Bounded By Curves (Using Definite Integrals) The Area A of the region bounded by the curves y = f(x), y = g(x) and the lines x = a, x = b, where f and g are continuous f(x) ≥ g(x) for all x in [a, b] is. The following diagrams illustrate area under a curve and area between two curves Oct 05,  · The area under the curve can be assumed to be made up of many vertical, extremely thin strips. Let us take a random strip of height y and width dx as shown in the figure given above whose area is given by dA. The area dA of the strip can be given as y dx. Also, we know that any point of the curve, y is represented as f(x).Estimated Reading Time: 2 mins